Longitudinal spectrum measurements of various lasers

Return to home page

• 633nm, 6mW HeNe laser, incl brief movie showing mode drift upon warmup and gain profile;
  
• 658nm, 80mW ML120G21 laser diode;
  
• 532nm, 100mW Coherent Compass 315M, incl movie showing mode jumps when running in an unstable regime;
  
• 532nm, 100mW GBS-100 DPSS laser
  
• 532nm, 10mW Picotronic DPSS module
  
• 532nm, 10mW DPSS laser pointer
  
• 488nm, 100mW NEC GLG3105 air cooled argon laser without etalon;
  
• 488/496/514nm, up to 500mW Lexel 88 argon laser with etalon - note the difference an etalon makes!
  There is also a brief movie that shows a scan through the longitudinal modes, done by tilting the etalon.
  
• 488nm/20mW Coherent Sapphire 488-20 OPSL laser displays stable single mode operation
• B&W Tek BWB-475-10-OEM DPSS laser runs in longitudinal multimode operation

General Remarks

For holography applications, one of the crucial features of a given laser is its coherence length. It determines the maximal depth a hologram made with the laser can have. For more information from this perspective, see the Holowiki. In brief, the coherence length is determined by the longitudinal mode structure, and therefore one can determine whether a given laser is good or not for holography, by determining its mode spectrum and the stability thereof (and of less importance, its line width).

For lasers with large cavities, the mode spacing is small (a few 100'sMhz) and the best device to measure it is a scanning Fabry-Perot interferometer (SFPI). Most measurements below were done with my home-made SFPI described in the link, and the piezo and mirror data that are sometimes given refer to that page.  

On the other hand, for small lasers with small cavities, eg DPSS lasers and especially laser diodes, the mode spacing of many Ghz is too large in order to be well captured by a SFPI (because the display becomes ambiguous as the modes "wrap around" it, and one would need a mirror spacing of a mm or so to prevent this); while one can see whether there are extra modes present or not, it is hard to judge their spacing, and thus, the actual coherence length. For such lasers, a grating based spectrometer is better suitable, and see here for a (partially) home-made device.

Right now I didn't yet obtain a lot of results using the grating based spectrometer (other than testing it), and its main application will be a thorough analysis of red laser diodes. Since this is a very complicated subject, and the reason for having the spectrometer in the first place, I devoted this page for specifically discussing spectral and stability properties of red diodes. It is expected to grow slowly over time.

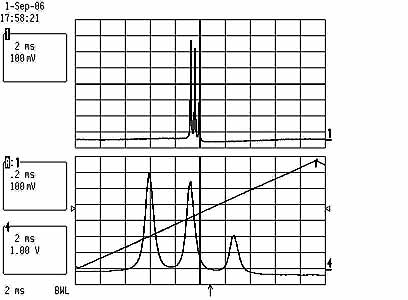
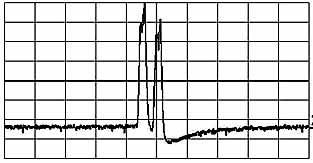
Testing a 633nm 6mW HeNe laser

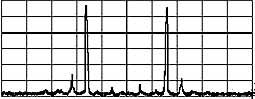
My scannning interferometer worked textbook-perfect for my small HeNe laser (unknown brand, ca 6.5mW). A few things could be learned:

• The resonator length is 38cm, so the mode spacing c/(2L) = 400Mhz. This fits very well into the 1.7Ghz free spectral range of the SFPI. From the pic below, this translates into approx 200Mhz/div on the scope screen, the total span being 2Ghz which is somewhat more than the FSR.


• From the ramp voltage displayed below (500V/div) this then translates to 1.4Ghz/500V, which amounts to 2.8Mhz per Volt scan width for the SMD1005T20 piezo element I used.
This means that in order to resolve a few Mhz, there must not be any AC ripple on the drive voltage on top of the sawtooth. My supply has less than oneVolt ripple at 700V, and this translates into a 1Mhz or so jitter on the screen.

• The lower trace shows a 10x zoom, which means 20Mhz/div. This tells that the resolution in the order of 10Mhz, which means that the finesse, or resolving power is 1.7Ghz/10Mhz = 170 - this is not at all bad for a SFPI made from surplus parts !


• In total one sees four longitudinal modes of the HeNe, and their span is approx 3 x 400Mhz = 1200Mhz. This translates to a coherence length of approx one-third of the HeNe resonator length, ie approx 13cm. This is an all-important quantity for holography, because depths larger than the coherence length cannot be recorded.

• While warming up one could see the modes drift, for more than 1/2 hour or so. In the beginning this was like 1div/sec, or 200Mhz/sec. Making holograms would clearly be impossible during that time. I would think that the drift during exposure time (10sec typ) should be small as compared to the mode spacing (400Mhz), so let's estimate the drift should be less than, say, 5Mhz/sec.
• Quite interesting is to make use of the mode drift during warm-up, and watch their amplitudes vary over the scan range. When storing all traces on the scope, this is gives a very direct way to see the gain profile of the laser. For my HeNe, it has a width of ca 1 Ghz:

I also recorded a little movie (QuickTime, 0.6MB) that shows how the mode drift builds up the above picture.

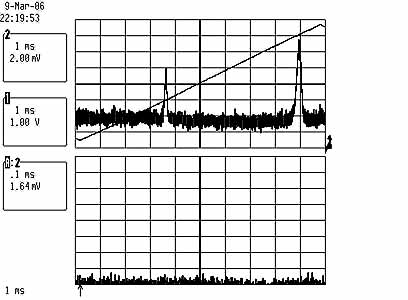
Testing a Mitsubishi ML120G21 658nm 80mW laser diode

Note added: since this is a very involved story, I devoted this page for specifically discussing spectral and stability properties of red diodes; it supersedes the following considerations.

• I spent quite some time at first to get a sensible pattern at all. The problem was a minute back reflection into the diode laser (despite slight off-axis adjustment) that had a quite dramatic effect, ie, a chaotic output; see the left pic below. Similar chaos obtains when the diode operates in an unstable zone (in the temperature/LD current plane), and during mode jumps that arise when changing the LD temperature by a very small amount.
  Only after placing an OD1 neutral density filter in front of the laser diode and very careful adjustmnent, a stable pattern occured (right pic below).
• The longitudinal mode spacing of a diode laser (100Ghz or so) is much larger than the free spectral range of the SFPI (1.7Ghz). Nevertheless, depending on whether there is a single or several peaks, can easily conclude whether the laser runs in single or multiple longitudinal mode. One cannot easily see what the frequency difference between multiple longitudinal modes is, but that's not important - we know the mode spacing approximately anyway, and this implies that whenever several longitudinal modes are visible, the laser is not suitable for holography. Moreover, one can easily see whether the diode output is chaotic or not.

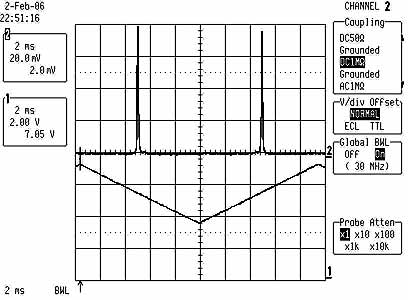
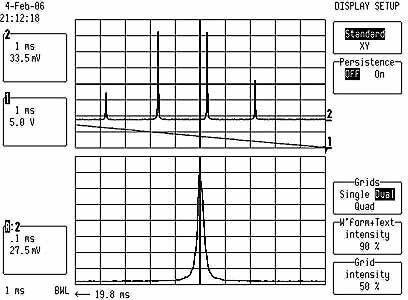
Left pic: chaotic laser diode output, when in unstable regime.

Right pic: super-clean spectrum of stable output, signalling single longitudinal mode operation.
Bottom lines indicate ramp voltage of piezo element (ca 300Vpp).

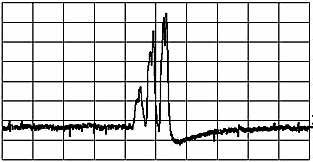
Testing a 532nm 100mW Coherent Compass 315M DPSS laser

• I used a pair of G3845-003 mirrors with index matched backsides, and got a finesse of the order of 200 with no difficulty. Back reflection into the laser did not pose any problem, no ND filter was needed, resulting in a strong signal despite the mirror being a high reflector.
• I used the larger piezo SMR2412T80, which gives approx two times FSR=1.5Ghz scan width.
• When running in a stable regime, the Compass 315M runs beautifully in single frequence mode, see picture below. This has been discussed at length at Sam's FAQ here and here. This confirms that the laser is excellent for holography use.

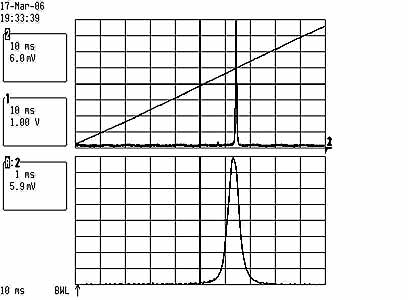
Clean single frequency mode operation of the Compass 315M at close to 100mW, total span is one FSR=1500Mhz.
Lower scale is zoomed 10 times and shows line width of approx 10Mhz; this means that the coherence length
is at least 10m or so (probably much more, as the limiting factor on the resolution is not the laser but the SFPI).

The above applies if the Compass 315M is running in a stable operating zone (mainly determined by LD current and
temperatures of KTP, resonator); see the notes in the Compass 315M measurements section.
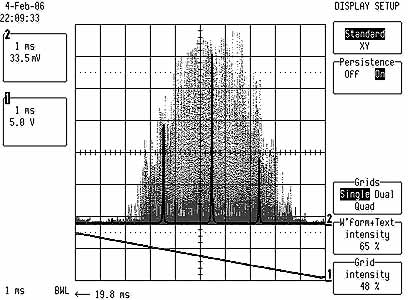
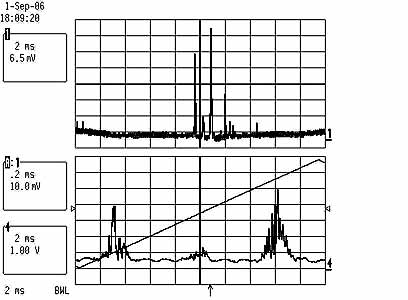
Below is a picture of the laser running in an unstable region where several modes are present:

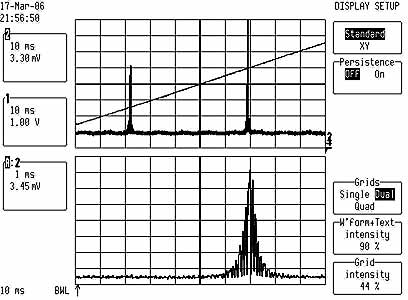
The zoom shows a fine substructure that I can't well explain, there seem to be some chaotic oscillations.
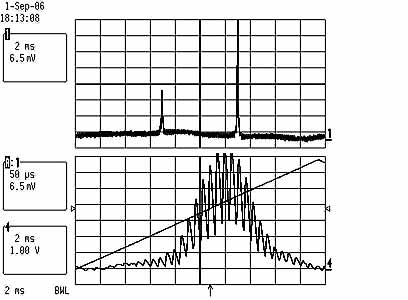
Here is a short QuickTime movie that shows the jumping of the modes when the KTP temperature is slightly changed,
in an unstable regime. It shows that this fine structure only appears when there are two peaks present within one FSR,
which is consistent with my interpretation.

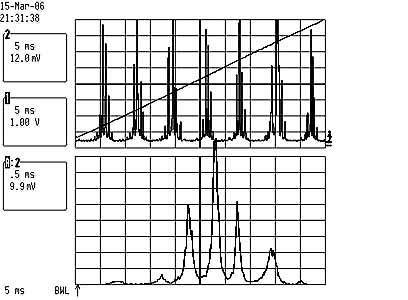
Testing a 532nm 100mW GBS-100 DPSS laser

• I bought it via ebay, and while it was not explicitly stated that this laser should do 100mW, it was very much suggested to be so. My measurements have found 75mW at the max, often just approximately 50mW. 
• I used the larger piezo SMR2412T80, which gives approx two times FSR=1.5Ghz scan width.
• It became immediately evident that the laser runs multi-mode, that is, two strong lines with almost equal strength plus a weak one. Their spacing strongly depends on the temperature, and I believe that it is too large to fit within one FSR. So what you see below is most likely a multiply wrapped spectrum, and the actual mode spacing is much larger; there is no simple way to figure this out from a SFPI. I may get better information with my grating based analyzer once that has been improved. At any rate, this confirms multimode operation that holographers suggested at holographyforum.org, who found striped patterns in holograms made with the GBS-100. Per se the laser is pretty stable due to its large thermal mass, and the mode drifting and hopping slows down after a short while.

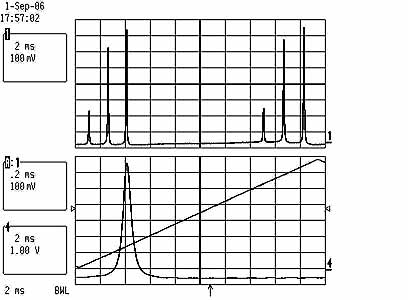
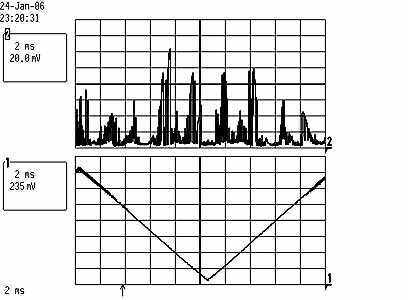
Left pic: Shown is two copies of the spectrum within one FSR=1.5Ghz; this corresponds to approx 200Mhz/Div. However, the apparent mode spacing of ca 200Mhz cannot be true, because this would correspond to a resonator length of roughly 1.5m. Rather, I think what is shown here is a multiply wrapped spectrum, for which the mode spacing is N*1.5Ghz+200Mhz, where N is unknown and hard to determine with the SFPI. Thus the coherence length is effectively at most a few cm only; the line width of a single mode (shown below at 10x zoom) is smaller than approx 10Mhz, which is good.

Right pic: While warming up, the mode spacing changes considerably, and at some point the three modes even appear to cross each other. Shown is here a single copy of the spectrum where the mode spacing appears to be only ca 30Mhz, which is impossible. The strong temperature dependence of the spacing supports the interpretation that the spectrum is displayed in a wrapped manner so that the spacing is N*1.5Ghz plus a small amount. In this way, a small relative change in the spacing (due to warm-up of the resonator), translates into a much larger apparent change.

I could reproduce the three modes with my CCD spectrum analyzer, and they look as follows:

Horizontal scale = 0.3nm/div, so the mode spacing is like 0.15nm, which amounts to 20Ghz and thus, to a coherence length of approximately 1.5cm.

Testing a 532nm 5mW DPSS Picotronic Module DD532-5-3

• Despite the (second-hand) seller claimed the module would do 10mW (twice the nominal 5mW), it did actually 2.5-3mW at arrival and now about 1mW after few hours of use....
• As expected, the modes drift and hop like crazy for a long time. As you see below, the spectrum is a mess and changes all the time. So the module is completely useless for holography, but this is no surprise. I'll use it for illuminating holograms anyway.

I could reproduce the two modes on the right with my CCD spectrum analyzer, and they look as follows:

Horizontal scale = 0.3nm/div.

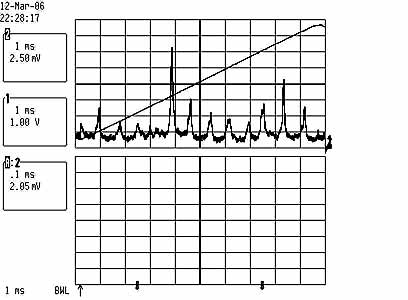
Testing a 532nm 10mW DPSS laser pointer

• Again using a pair of G3845-003 mirrors with index matched backsides.
• Adjustment and recording was difficult and non-optimal as I didn't want to run the pointer for long time.
  Thus the modes moved across the screen because the pointer didn't get in thermal equilibrium.
• Often several lines appeared, signalling non-single frequency mode (see pic below).
  Because the mode spacing is much larger than the free spectral range of the SFPI,
  the display wraps around a few times, and so one cannot read off the true frequency difference between the modes.
  But one can easily verify that several modes are present, which means that this laser is unsuitable for holography.

Testing a 488nm 100mW NEC GLG3105 air cooled argon laser

• This is for an old tube tested at 30mW.
• I used the larger piezo SMR2412T80, which gives approx two times FSR=1.5Ghz scan width.
• I used a pair of G3845-002 mirrors with index matched backsides.
• This air cooled laser has internal mirrors and no etalon.
  Not surprisingly, it runs many longitudinal modes, which means: "No good for holography" !

This picture shows a quite messy multi-longitudinal mode output.
The scale is approx 350Mhz/div, and this fits well to a longitudinal mode spacing of 510Mhz (29.5cm res length).
The picture covers slightly more than two FSR=1.5Ghz, so we get two repetitions of the same spectrum.

Actually the story is more complicated than that: there are many secondary peaks,
and despite these look like if they would come from a misaligned SFPI, their distance does
not change when changing the mirror spacing. Thus they really must be due to modes coming from the laser.
Note that the FSR is approx 1.5Ghz which is pretty accurately three times the mode spacing (510Mhz) of the laser.
This means the laser modes outside a free spectral range will map back pretty closely onto the lines within one FSR,
within approx 30Mhz, and this is indeed consistent with what I find for the spacing of the smaller peaks!
(see the 10 times zoomed lower part of the pic).

So all this is consistent with a multi-longitudinal mode output spanning many Ghz, and thus, with just a few cm of coherence length.

Testing a Lexel 88 Argon Laser

• This is for my OEM Lexel 88 retrofitted with an original Lexel etalon.
• For 514nm I used a pair of G3845-003 mirrors with index matched backsides, which produced an
  extremely weak signal due to the high reflectivity. Only running at 100mW I could get a decent signal out.
• For 488nm and 496nm I used a pair of G3845-002's. These work just marginally for 488nm, and this only after I had
  first fully adjusted the SFPI for 496nm - I was not able to find the right spot for 488nm due to
  the extremely weak signal in the first place.
• I used the larger piezo SMR2412T80, which gives approx two FSR=1.5Ghz scan width.

------------ 488nm:-------------

• Surprisingly, while single frequency mode was easy to achieve at 514nm and 496nm,
  I could not achieve a clean output for 488nm - see below. I presume this is because either the etalon is not
  optimized for 488nm, or more likely, it is due to the non-original mirrors I am using.
  This was a quite unexpected outcome of the whole exercise - with this current setup,
  I won't be able to use the 488nm line for holography!

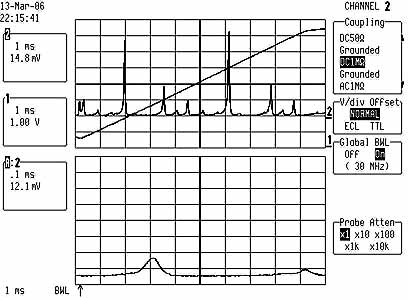
Left picture: multi-mode output at 488nm with careless adjustment of the etalon.
The distance between the peaks corresponds to approx 200Mhz, which is the mode spacing of the laser cavity.

Right picture: even careful adjustement of the etalon does not fully get rid off the extra modes.
The scan captures about two FSR=1.5Ghz, so the large peaks are multiple copies of the same line.

------------ 496nm:-------------

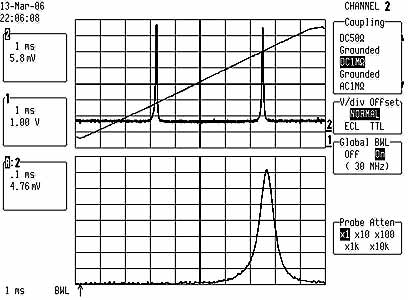
Clean single frequency output at 496nm. Upper part: ca 350Mhz/div, lower part: 35Mhz/div.

------------ 514nm:-------------

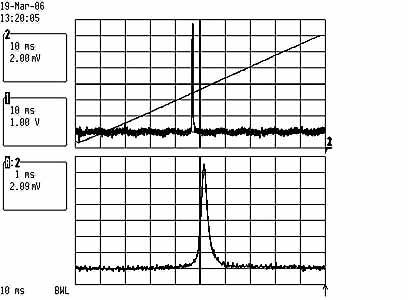
Left picture: Single frequency output at 100mW. The scan width is one FSR=1.5Ghz, and from the lower
zoomed part with 15Mhz/div we see a line width of approx 5Mhz. Thus the finesse of the SFPI
is in the order of excellent 300! This also means that the coherence length is at least in the order of several tens of meters.

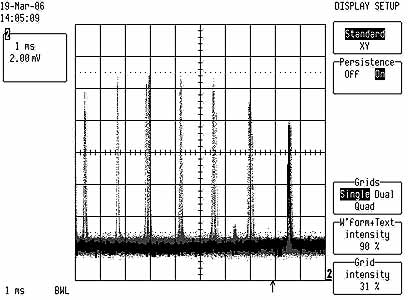
Right picture: By slowly tilting the etalon, the laser jumps from one longitudinal mode to the next.
Shown is a scan over these modes obtained in this way.
Their spacing is f=200Mhz, which corresponds to the resonator length L=76cm of the laser (f=c/(2L)).
Here is also a brief QuickTime movie that shows how these mode jumps were recorded.

Coherent Sapphire 488-20 OPSL

It displays nice stable single mode operation near 488nm at 20mW, practically over all power settings. Shown below a pic of the scanning interferometer output:

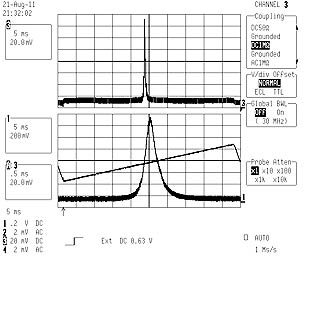
Lower trace is 10-fold zoom of upper trace, ie, approx 20Mhz/Div. The line width thus is in the order of at most 20Mhz, and so the coherence length at least several dozens of meters!

For some further details see here.

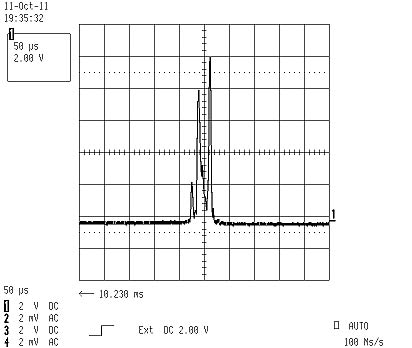
B&W Tek BWB-475-10-OEM DPSS laser

I got one of those "out of specs", it hat 5mW at 475nm, instead of 10mW. As expected the nice little thingy runs multimode and thus is unusuable for holography purposes. Shown is the output of my CCD spectrum analyzer:

Return to home page

Vers 1.3 -10/11